4 Modelado espacial diario de \(\Psi_s\)
4.1 Predictores espacio-temporales
Variables meteorológicas
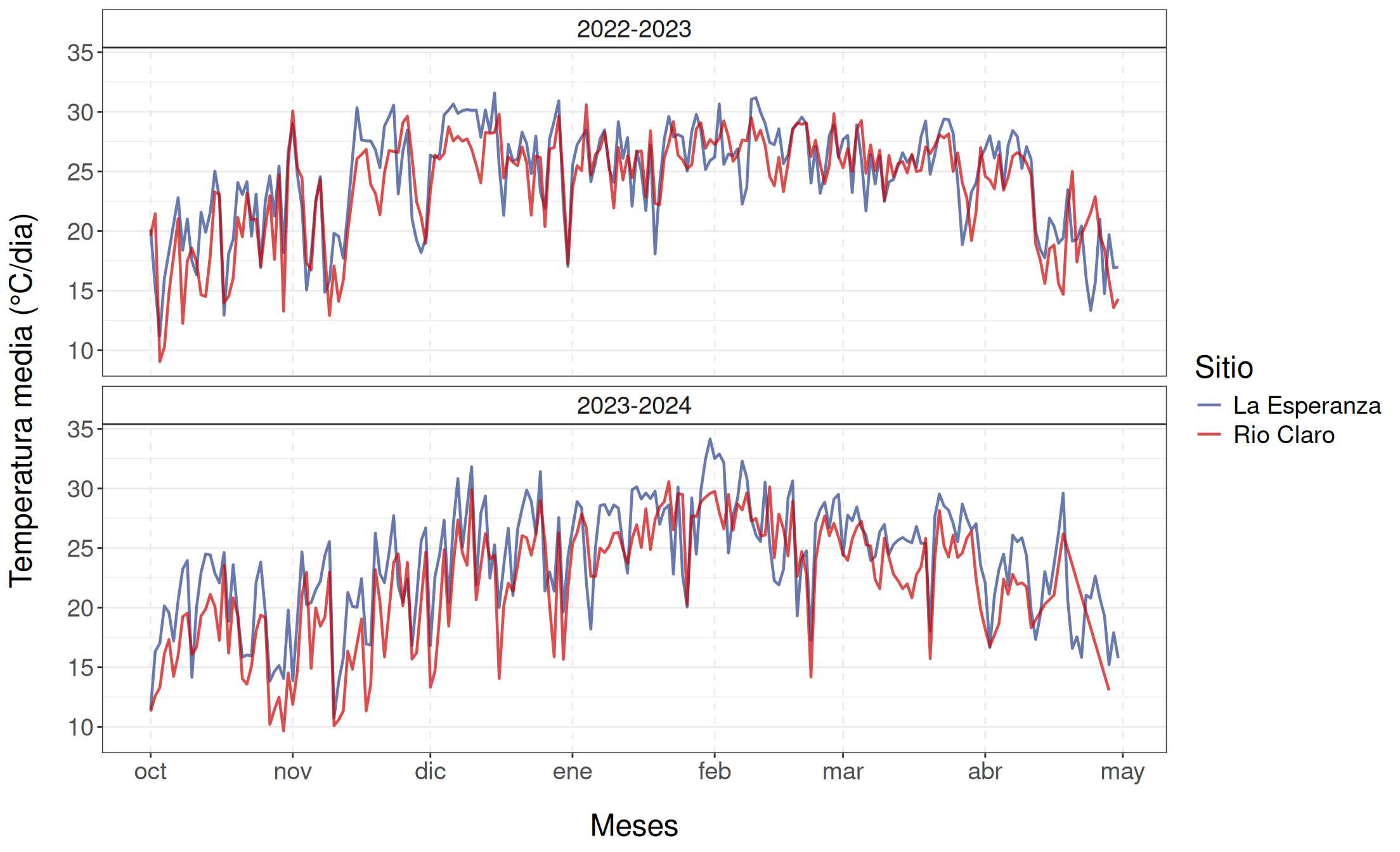
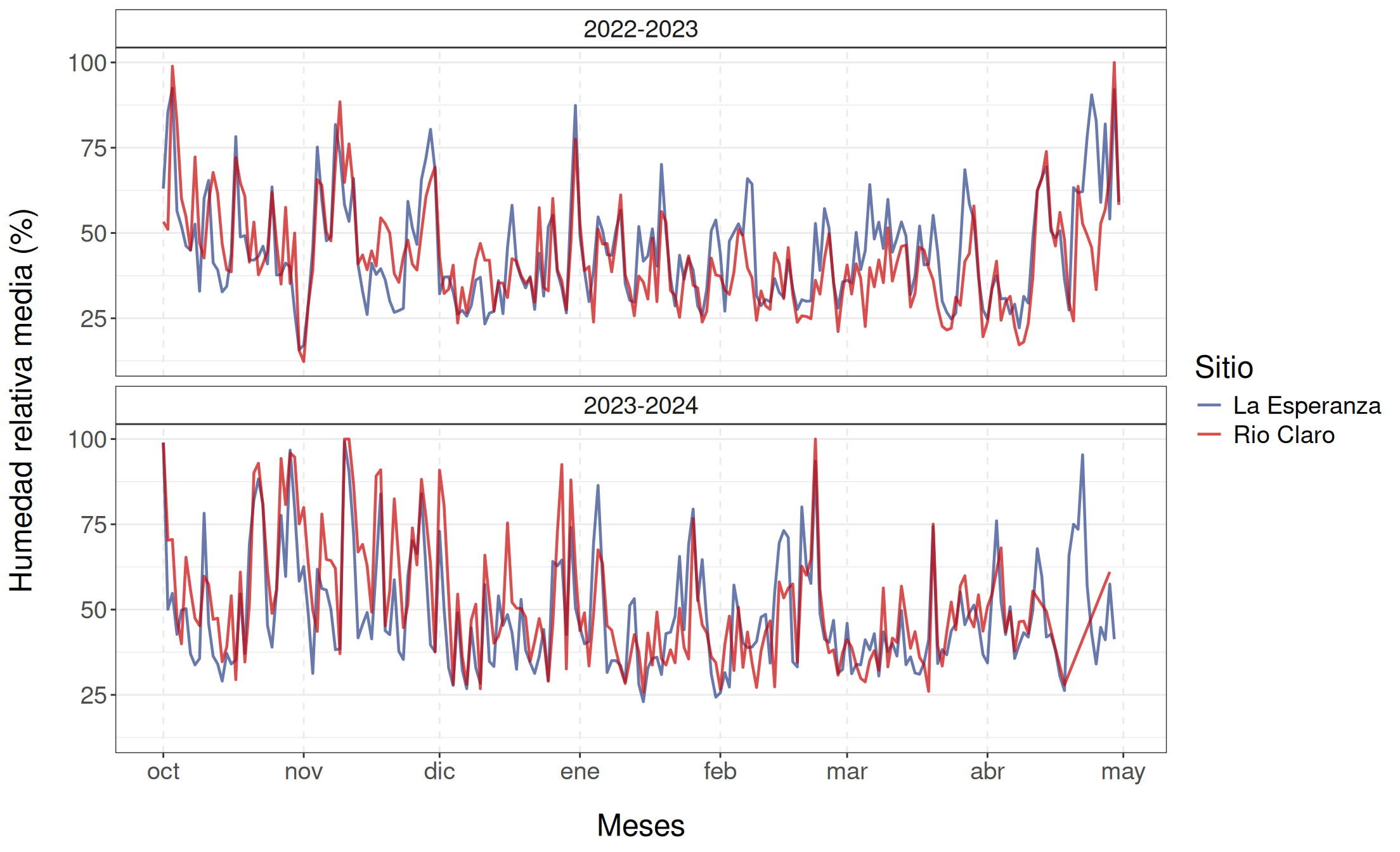
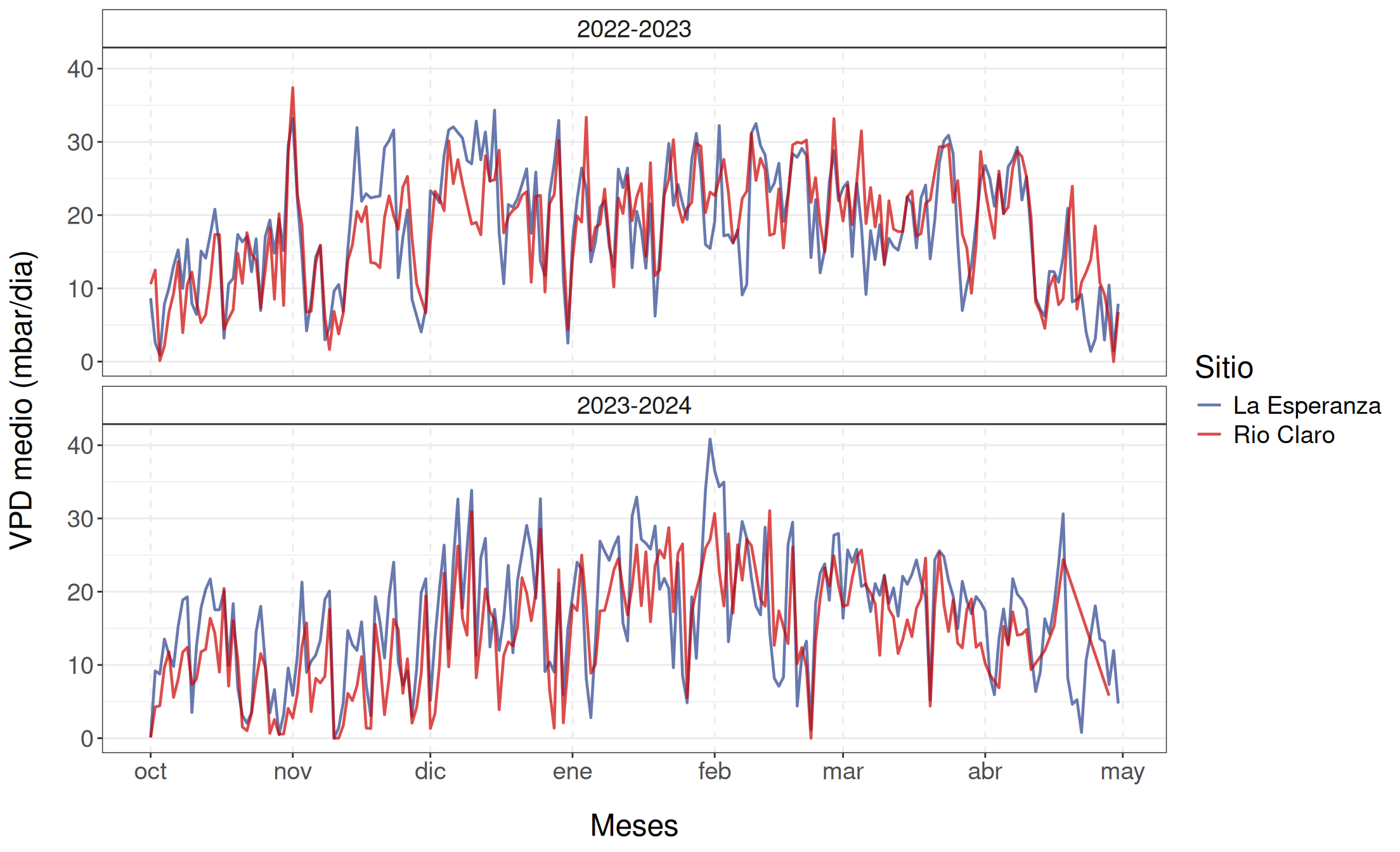
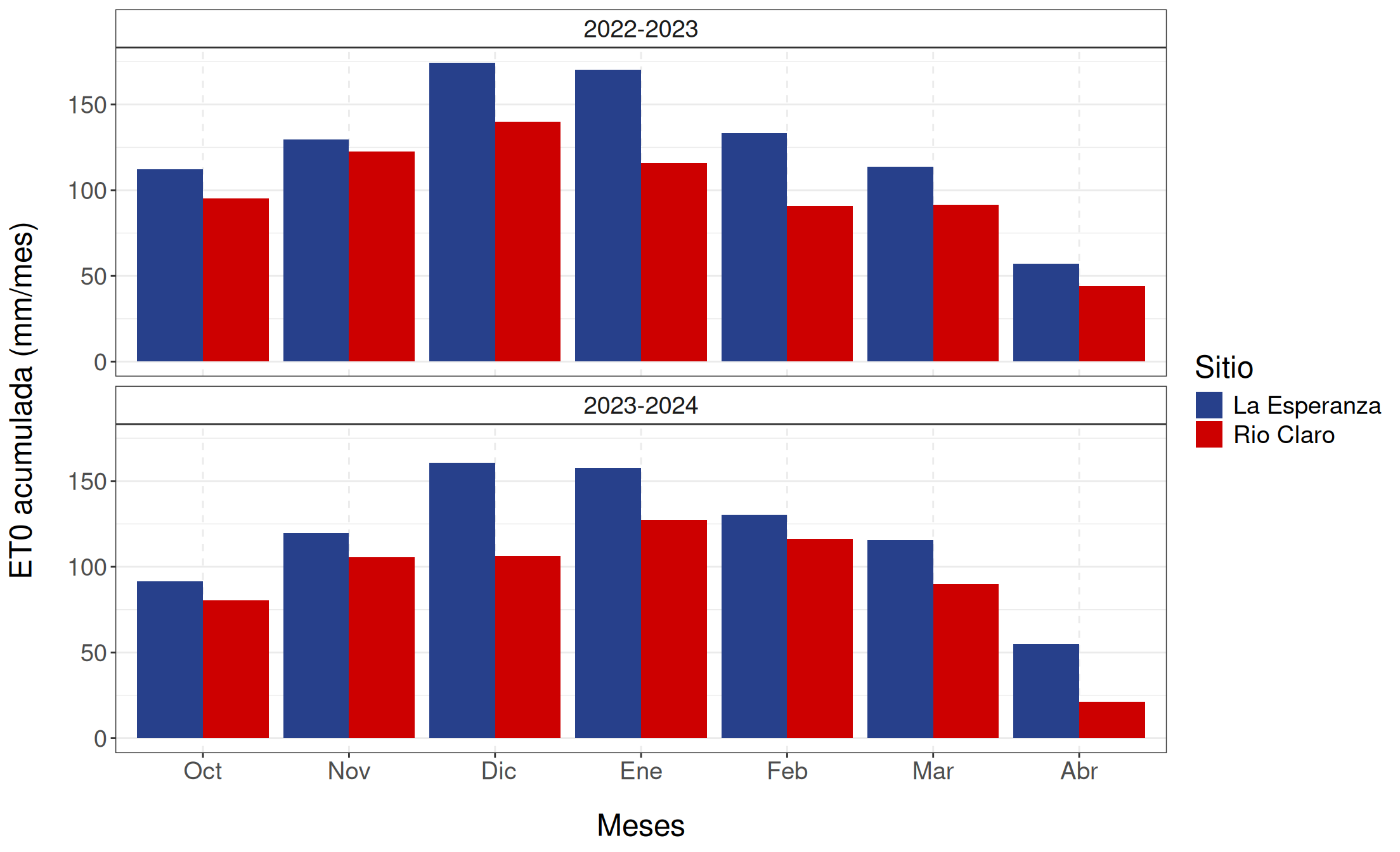
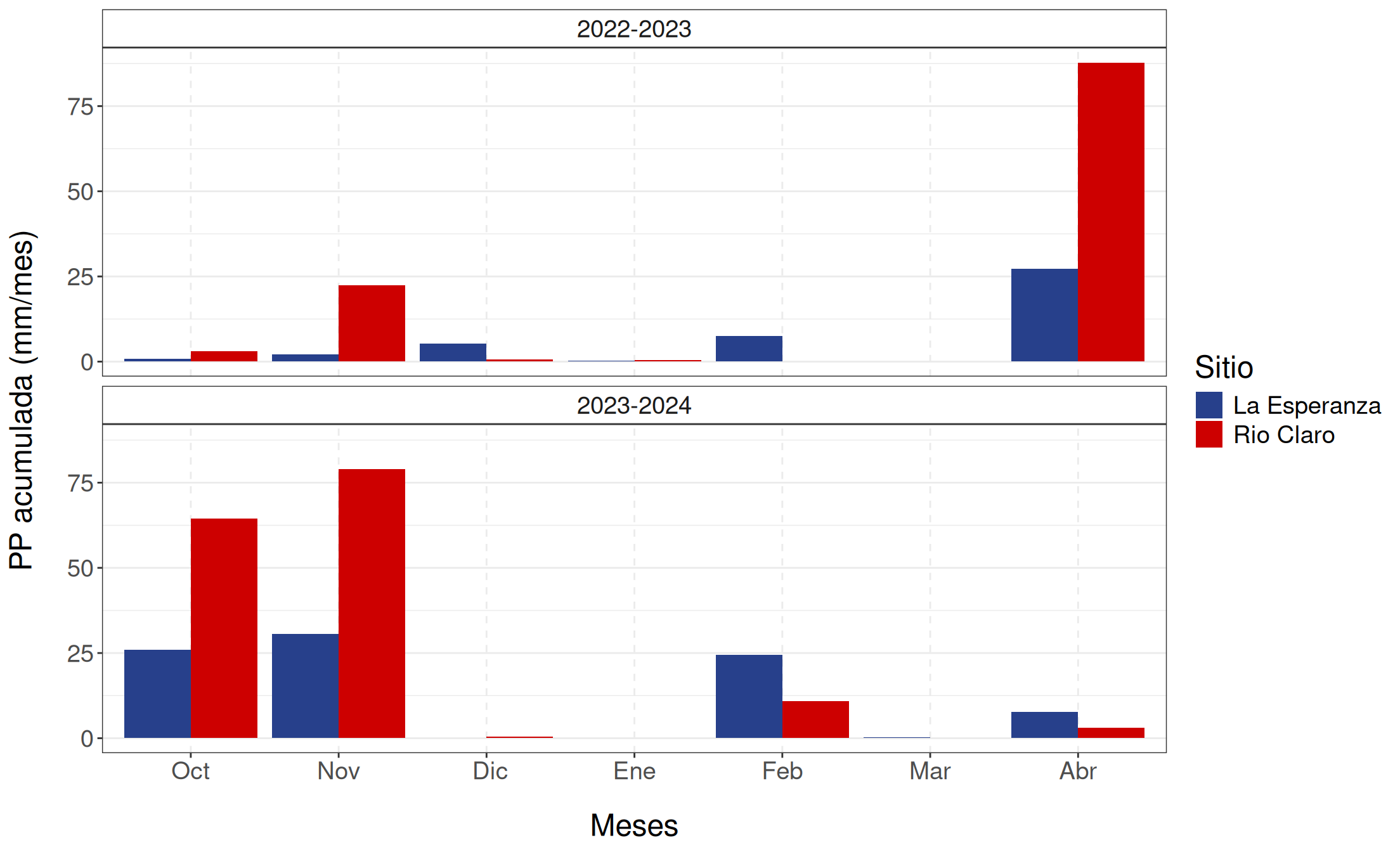
Las variables meteorológicas utilizadas en el desarrollo del modelo de \(\Psi_s\) se obtuvieron a partir de estaciones meteorológicas automáticas en ambos huertos, las cuales registraron datos cada 15 minutos utilizando el modelo ATMOS-41 del grupo METER. Estas variables fueron temperatura (\(T\)), humedad relativa (\(HR\)), déficit de presión de vapor (\(VPD\)), precipitación (\(PP\)) y evapotranspiración de referencia (\(ET0\)).
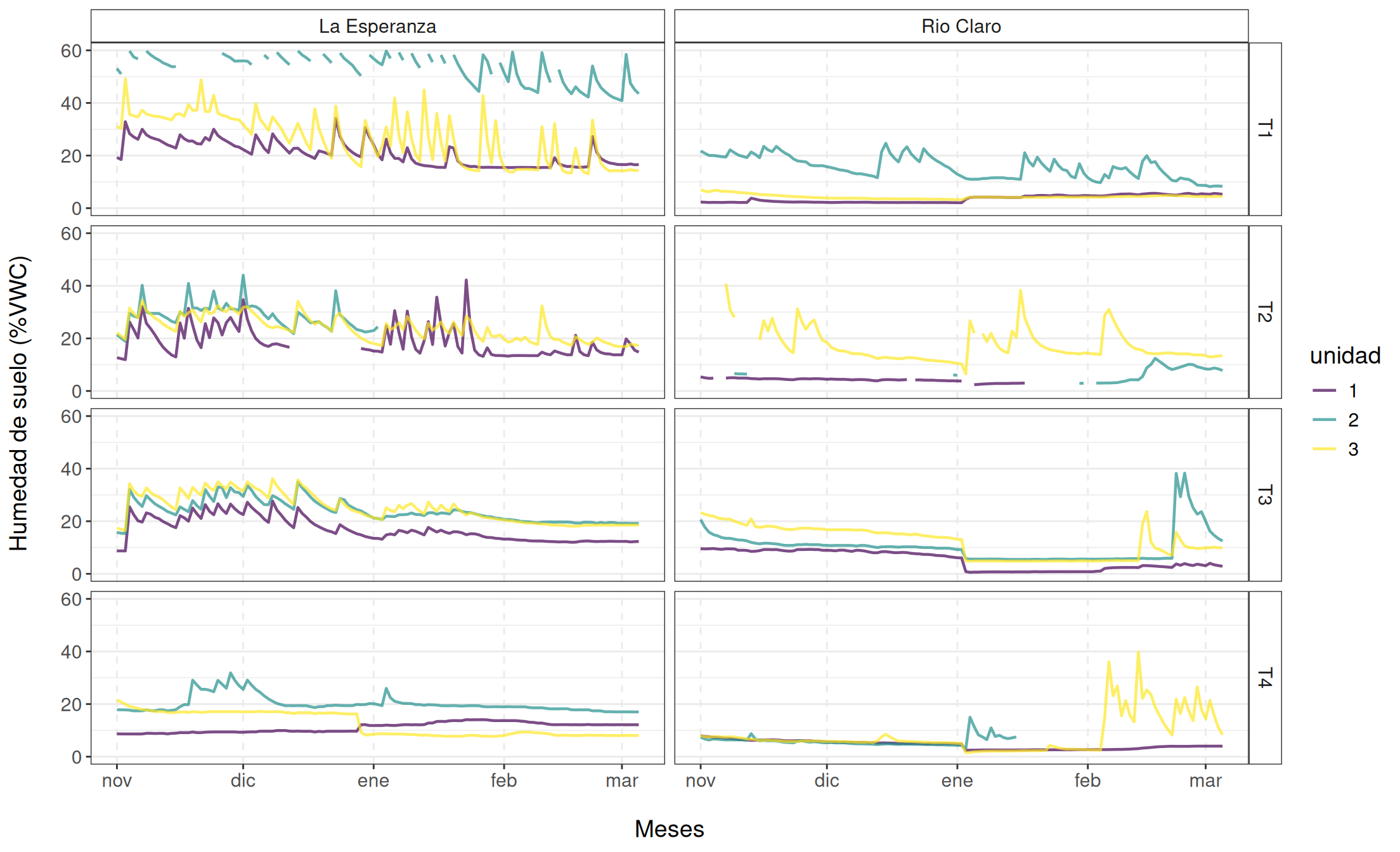
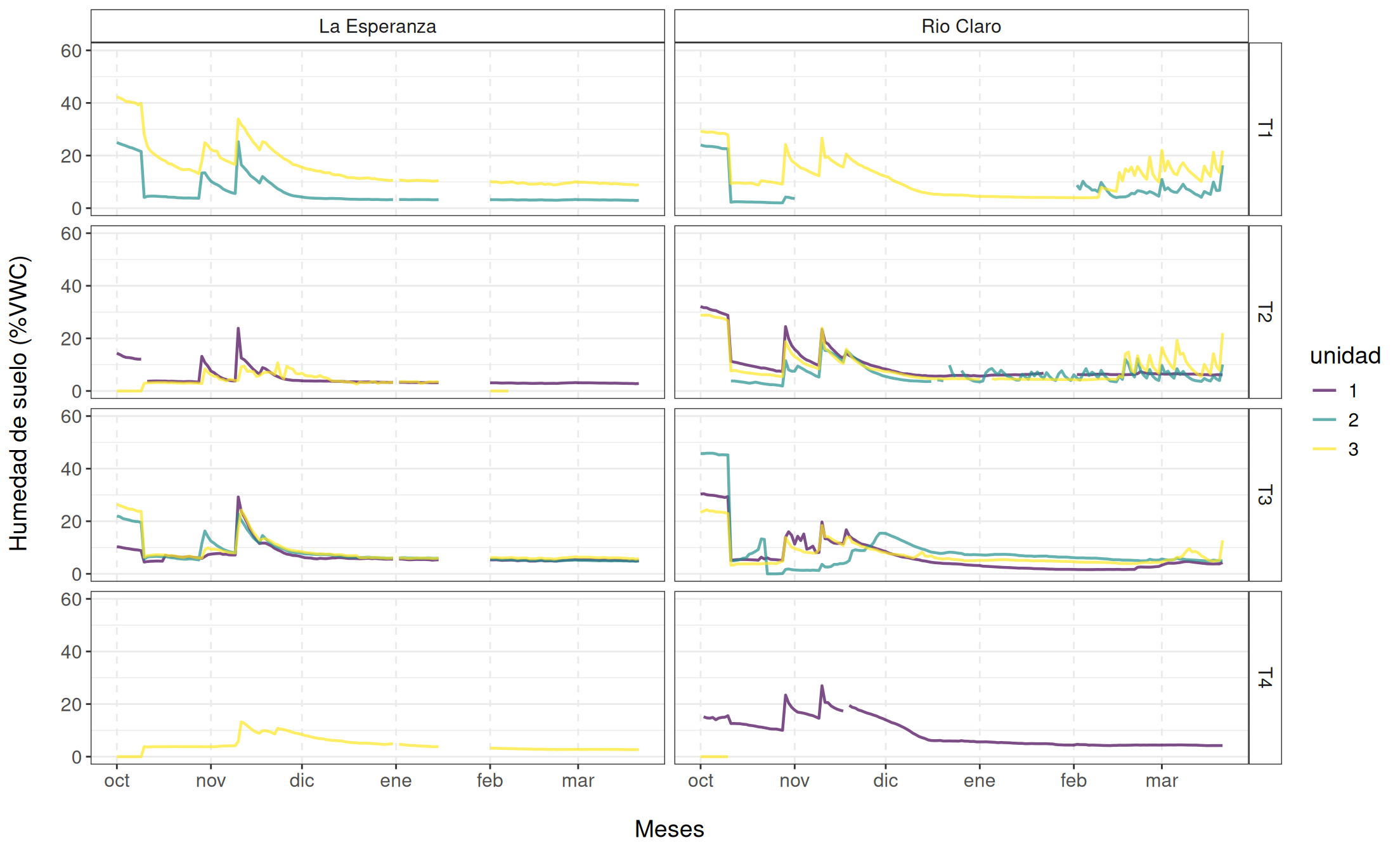
Además de las variables meteorológicas, también se recopilaron datos de humedad del suelo. Para esto, se utilizaron sensores de humedad del suelo Water Scout SM100 (Spectrum Technologies, Inc.), los cuales miden en tiempo real el contenido volumétrico de agua (VWC). Estos sensores se instalaron a 15 cm de profundidad bajo cada árbol de los tratamientos.
Datos de teledetección y IVs
Para obtener variabilidad espacial en el modelamiento de \(\Psi_s\), se utilizó información satelital a partir del satélite Sentinel-2 (S2). La misión S2 consta de dos satélites idénticos, S2A y S2B, ambos equipados con un sensor multiespectral que cuenta con 13 bandas espectrales que cubren las regiones visible, infrarrojo cercano e infrarrojo de onda corta, con resoluciones espaciales de 10, 20 y 60 m (ver Tabla S2). En este estudio, utilizamos un total de 106 imágenes S2 (A/B): 54 para la temporada 2022-2023 y 52 para la 2023-2024, capturadas entre octubre y mayo en ambos huertos (cuadrícula T19HCB para La Esperanza y T19HBB para Río Claro). Las imágenes se obtuvieron de la colección corregida atmosféricamente S2 Level-2A de Planetary Computer (Microsoft Open Source et al. 2022), con una frecuencia de 5 días y aproximadamente a las 14:30 hora local (UTC-4). Una máscara fue aplicada basandose en la capa de clasificación de escena (SCL) para los valores correspondientes a “Cloud Shadows,” “Cloud Medium Probability,” y “Cloud High Probability,”.
A partir de estos datos de S2, se derivaron dieciséis índices de vegetación (IVs) relacionados con la condición de las plantas vigor, estrés, funcionalidad fotosintética y contenido hídrico. De estos, nueve índices no incorporaron información del red-edge (borde rojo), calculándose exclusivamente con bandas espectrales del visible, infrarrojo cercano (NIR) e infrarrojo de onda corta (SWIR): NDVI, EVI, GCI, NDWI, NBR, NDMI, MSI, NMDI y DWSI. Por otro lado, siete índices —CLr, Clg, NDRE1, NDRE2, NDCI, mSR705 y RESI— se obtuvieron mediante las bandas del red-edge. Todos los índices fueron calculados a partir de las imágenes preprocesadas de las bandas de S2, generándose series temporales para cada IV en ambos huertos y temporadas.
Para reconstruir las series temporales (ej. en zonas afectadas por nubosidad), se aplicó un suavizado mediante regresión polinomial local (LOESS) (Cleveland 1979). El método LOESS se configuró con un parámetro de suavizado (span) de 0.3, obteniéndose así series diarias continuas y suavizadas para cada índice, las cuales posteriormente fueron extraídas para cada árbol medido. Se llevó a cabo un análisis de correlación para evaluar la relación entre estas series suavizadas y los valores observados de \(\Psi_s\). El coeficiente de correlación de Pearson (\(r\)) fue calculado diariamente para cada árbol, huerto y temporada, utilizando exclusivamente correlaciones significativas (p-value < 0.05) para el cálculo de los valores promedio.
4.2 Modelos de machine learning
Para modelar el \(\Psi_s\), se evaluaron tres algoritmos de machine learning:
- Extreme Gradient Boosting (XGBoost; Chen y Guestrin (2016))
- Random Forest(RF; Tin Kam Ho (1995))
- Support vector Machine (SVM; Cortes y Vapnik (1995))
Los dos primeros métodos se basan en árboles de decisión, mientras que el tercero utiliza vectores de soporte. Estos modelos fueron seleccionados por ser considerados de vanguardia, requerir un número reducido de muestras de entrenamiento (en comparación con redes neuronales) y ofrecer interpretabilidad. Todos los algoritmos pueden emplearse tanto para clasificación como para regresión. En este estudio, se realizó un análisis de regresión, utilizando el \(\Psi_s\) como variable respuesta y 21 predictores: cinco meteorológicos y 16 índices de vegetación (IVs).
El conjunto de datos incluyó mediciones de 26 fechas en la temporada 2022–2023 y 34 en la 2023–2024 (total: 60 fechas). Para cada fecha, se tomaron 30 mediciones (15 por huerto: Río Claro y La Esperanza), lo que resultó en un total de 883 observaciones. El proceso de modelado siguió las siguientes etapas:
- Preparación y división de datos: Segmentación del conjunto de datos en subconjuntos de entrenamiento y prueba.
- Optimización de hiperparámetros: Ajuste de los parámetros de los algoritmos utilizando el conjunto de entrenamiento.
- Remuestreo: Evaluación de la confiabilidad del modelo e identificación de las variables más relevantes para estimar \(\Psi_s\).
- Validación: Evaluación del rendimiento del modelo con métricas de desempeño.
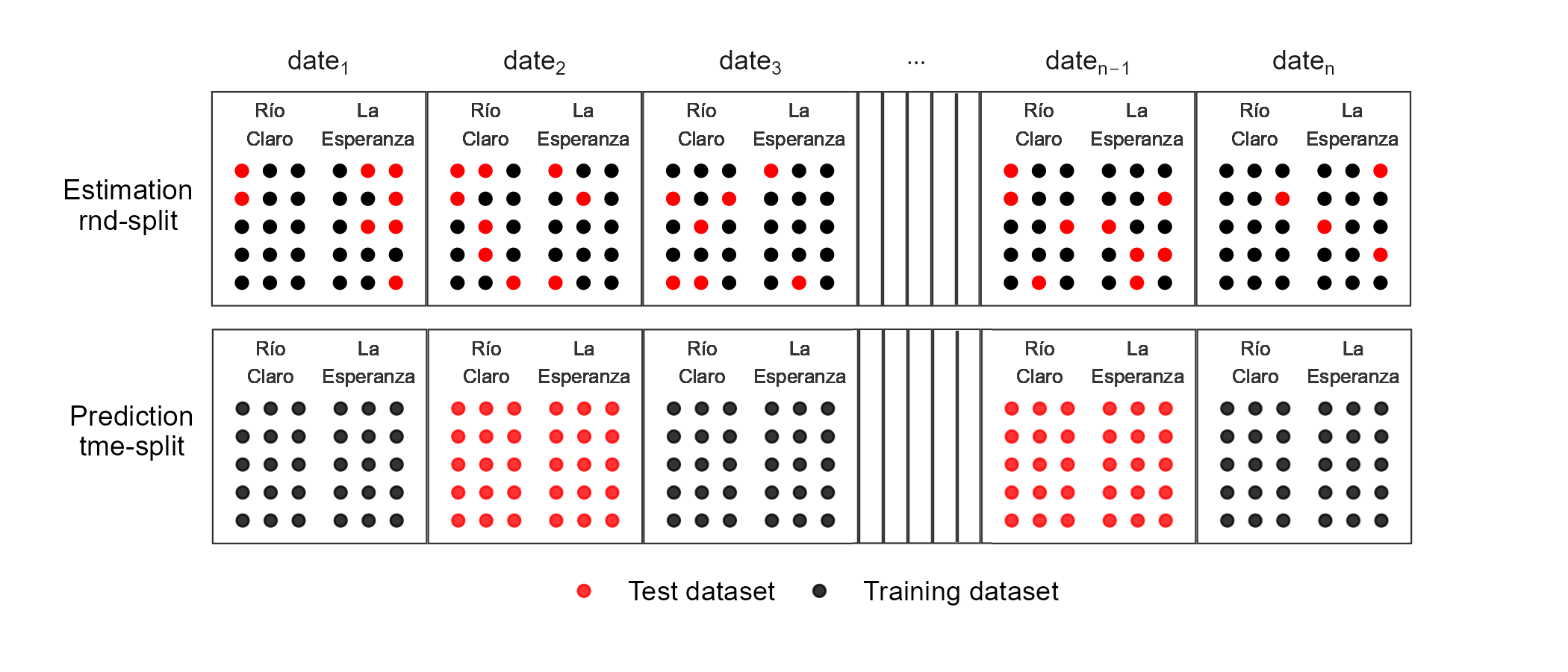
Se entrenaron los tres modelos utilizando dos esquemas de división (Figura 4.8): uno que consideró una división aleatoria de datos de entrenamiento y prueba (rnd_split) y otro que utilizó fechas independientes para entrenamiento y prueba (tme_split). En ambos casos, se seleccionó el 75% de los datos para entrenamiento y el 25% para prueba. Se aplicaron tres tipos de preprocesamiento a los datos de entrenamiento: i) eliminación de predictores con valores constantes (variables de varianza cero); ii) normalización de predictores (media cero y desviación estándar uno); y iii) una versión del modelo que empleó Partial Least Squares (PLS) para reducir la dimensionalidad, utilizando las cinco componentes principales como predictores. Como resultado, se usaron modelos con predictores normalizados y otros con las componentes principales de PLS.
Para ajustar los parámetros de los modelos (XGBoost, RF, SVM), se empleó optimización de hiperparámetros. Se definieron rangos para cada parámetro y se utilizaron cinco folds de validación cruzada para ambos esquemas de división (rnd_split y tme_split). La optimización evaluó diez combinaciones de parámetros por modelo. El rendimiento se midió con las métricas R², RMSE (root-mean-square error) y MAE (mean absolute error). Finalmente, los modelos se clasificaron según el RMSE más bajo y el R² más alto, seleccionándose aquellos con mejor desempeño.
4.3 Evaluación e importancia de los modelos
Para evaluar el rendimiento de los modelos, se aplicó remuestreo (resampling) sobre el conjunto de entrenamiento en ambos esquemas de división (rnd_split y tme_split). Se utilizaron cinco particiones y se calcularon las métricas R², MAE (Error Absoluto Medio) y RMSE (Raíz del Error Cuadrático Medio) para cada una de estas.
En cuanto a la importancia de variables, el modelo de Bosques Aleatorios (RF) empleó un método de permutación out-of-bag en cada árbol, permutando los predictores y calculando el error cuadrático medio para cada instancia. Para XGBoost, se estimó la contribución fraccional de cada variable según la ganancia total en las divisiones donde participó. En el caso de SVM, se calcularon puntuaciones de importancia basadas en permutaciones (para más detalles, véase Greenwell y Boehmke (2020)).